vektor.jenis vektor,operasi vektor dan contoh soalnya

 

Pengertian Vektor

Vektor  adalah merupakan sebuah besaran yang memiliki arah. Vektor digambarkan sebagai panah dengan yang menunjukan arah vektor dan panjang garisnya disebut besar vektor. Di dalam penulisannya, jika vektor berawal dari titik A dan berakhir di titik B bisa ditulis dengan sebuah huruf kecil yang diatasnya ada sebuah tanda garis/ panah seperti atau  atau juga:

Lihat juga materi Gurusekolah.co.id lainnya:
Rumus deret aritmatika-Pengertian dan Rumus Serta Contoh Soalnya
Energi-Pengertian Energi Dan Jenis – Jenis Energi Lengkap

Misalkan vektor  adalah merupakan vektor yang berawal dari titik  menuju titik  dapat juga digambarkan koordinat cartesius dibawah. Panjang garis sejajar sumbu x ialah  dan panjang garis sejajar sumbu y ialah   adalah merupakan komponen-komponen vektor .

Pada komponen vektor  dapat ditulis untuk menyatakan vektor secara aljabar yaitu:

Jenis-jenis Vektor

Ada beberapa jenis-jenis vektor khusus yaitu:

• Vektor Posisi
  Yaitu Suatu vektor yang posisi titik awalnya di titik 0 (0,0) dan titik ujungnya di A 
• Vektor Nol
  Yaitu Suatu vektor yang panjangnya nol dan dinotasikan . Vektor nol tidak memiliki arah vektor yang jelas.
• Vektor satuan
  Pada suatu vektor yang panjangnya satu satuan. Vektor satuan dariadalah         

Vektor di R^2

Panjang segmen garis yang menyatakan vektor  atau dinotasikan sebagai Panjang vektor adalah:

Panjang vektor juga dapat dikaitkan dengan sudut  yang dibentuk oleh vektor dan sumbu x, positif

Vektor dapat disajikan sebagai kombinasi linier dari vektor basis  dan berikut:

Operasi Vektor di R^2

Penjumlahan dan pengurangan vektor di R^2

Dua vektor atau lebih dapat juga dijumlahkan dan hasilnya disebut resultan. Penjumlahan vektor secara aljabar dapat dilakukan dengan cara menjumlahkan komponen yang seletak. Jika  dan  maka:

Penjumlahan secara grafis dapat dilihat pada gambar dibawah:

Dalam pengurangan vektor, berlaku sama dengan penjumlahan yaitu:

Sifat-sifat dalam penjumlahan vektor sebagai berikut:

• 
• 

Perkalian vektor di R^2 dengan skalar

Suatu vektor dapat dikalikan dengan suatu skalar (bilangan real) dan akan menghasilkan suatu vektor baru. Jika  adalah vektor dan k adalah skalar. Maka perkalian vektor:

Dengan ketentuan:

• Jika k > 0, jadi vektor  searah dengan vektor 
• Jika k < 0, jadi vektor  berlawanan arah dengan vektor 
• Jika k = 0, jadi vektor  adalah vektor identitas 

Secara grafis perkalian ini dapat juga merubah panjang vektor dan dapat dilihat pada tabel dibawah:

Secara aljabar perkalian vektor  dengan skalar k dapat juga dirumuskan:

Perkalian Skalar Dua Vektor di R^2

Perkalian skalar dua vektor dapat disebut juga sebagai hasil kali titik dua vektor dan ditulis sebagai:

 (dibaca : a dot b)

Perkalaian skalar vektor  dan  dilakukan dengan mengalikan panjang vektor  dan panjang vektor  dengan cosinus . Sudut  yang adalah merupakan sudut antara vektor dan vektor .

Sehingga:

Dimana:

Perhatikan bahwa:

• Hasil kali titik dua vektor menghasilkan suatu skalar
• 
• 

Vektor di R^3

Vektor yang berada pada suatu ruang tiga dimensi (x, y, z).jarak antara dua titik vektor dalam  dapat diketahui dengan pengembangan rumus phytagoras. Jika titik  dan titik  maka jarak AB adalah:

Atau jika , maka

Vektor  dapat juga dinyatakan dalam dua bentuk, yakni dalam kolom  atau dalam baris . Vektor juga dapat disajikan sebagai kombinasi linier dari vektor basis  dan  dan  berikut:

Operasi Vektor di R^3

Operasi vektor di  yang secara umum, mempunyai konsep yang sama dengan operasi vektor di  dalam penjumlahan, pengurangan, maupun perkalian.

Penjumlahan dan pengurangan vektor di R^3

Penjumlahan dan pengurangan dari vektor di  sama dengan vektor di  yaitu:

Dan

Perkalian vektor di R^3 dengan skalar

Jika  adalah vektor dan k adalah skalar. Maka perkalian vektor:

Hasil kali skalar dua vektor

Selain pula rumus di , ada juga rumus lain dalam hasil kali skalar dua vektor. Jika  dan  maka  adalah:

Proyeksi Orthogonal vektor

Jika vektor  diproyeksikan pada vektor  dan diberi nama  seperti gambar dibawah:

Diketahui:

Sehingga:

 atau 

Untuk mendapat vektornya:

Contoh Soal Vektor Matematika

Contoh Soal 1

Jika diketahui bahwa vektor dititik A serta dititik B dan juga vektor dititik C itu terletak diantara garis Ab sama seperti dengan yang ada pada gambar dibawah ini.

aka tentukanlah persamaan dari sebuah vektor C ini.

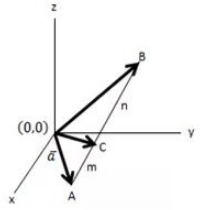
Jawaban :

Menurut gambar diatas itu dapat diketahui apabila :

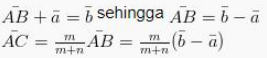
Kemudian :

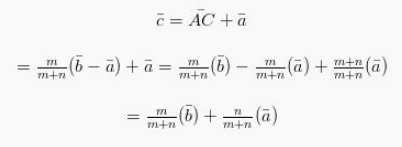
Contoh Soal 3

Apabila diketahui bahwasannya sebuah titik pada A(2,4,6), B(6,6,2), dan C(p,q,-6).

Dan jika titik A, B juga C ini terletak segaris, maka carilah berapakah nilai dari p+q tersebut ?

Jawaban :

Apabila titik titik pada A, B serta C ini segaris, maka vektor pada AB dengan vektor pada AC itu juga bisa searah atau bahkan berlainan arah.

Baca Juga : Fungsi Komposisi

Kemudian akan ada bilangan m yang menjadi sebuah kelipatan juga bisa membentuk sebuah persamannya misalnya seperti dibawah ini :

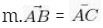
Jika B berada diantara titik A dan juga C, maka bisa didapatkan menjadai seperti dibawah ini :

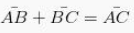
Kemudian akan bisa ddapatkan :

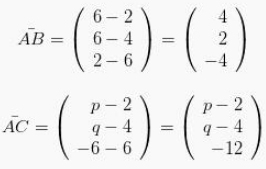
Selanjutnya bisa ditentukan kekelipatan m didalam sebuah persamaan yaitu :

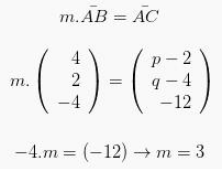
Dan hasil yang akan didapatkan yakni :

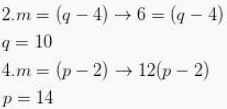
Dan bisa ditarik kesimpulan seperti : p+q=10+14=24.