SIFAT KESIMETRIAN DAN SIFAT SUDUT PADA SEGITIGA,SIFAT SEGI EMPAT DAN LINGKARAN BERSAMA CONTOH SOALNYA

NAMA: ANGGUN INDAH SARI DARMAYANTI

 Simetri adalah karakteristik bangun geometri yang jika diterapkan tidak akan muncul suatu perubahan. Ada dua macam simetri pada bangun datar, yaitu simetri lipat dan simetri putar. Yuk, kita bahas apa sih itu simetri lipat dan simetri putar. Simetri lipat adalah jumlah lipatan yang dapat dibentuk bangun datar menjadi dua bagian sama besar. Sedangkan, simetri putar adalah jumlah putaran yang dapat dibentuk bangun datar dimana hasil putarannya membentuk pola yang sama, namun tidak kembali ke posisi awal.

Nah, sudah pahamkan apa itu simetri lipat dan simetri putar. Sekarang, kita bahas bangun datar Segitiga, Segiempat, dan Lingkaran, serta pengaplikasian simetri lipat dan simetri putar ke ketiga bangun datar tersebut.

Segitiga

Segitiga adalah bangun datar yang terdiri dari tiga garis lurus dengan tiga sudut yang berjumlah 180°. Segitiga ternyata punya klasifikasinya loh Greaters! Kita bedah satu-satu ya, yuk kita simak bersama ya!

Klasifikasi Segitiga Berdasarkan Panjang Sisi

1) Segitiga Sama Sisi

Segitiga sama sisi adalah segitiga yang mempunyai sisi sama panjang sehingga tiap sudutnya berukuran 60°. Segitiga sama sisi mempunyai tiga simetri lipat dan tiga simetri putar.

2) Segitiga Sama Kaki

Segitiga sama kaki adalah segitiga yang mempunyai dua sisi sama panjang, sehingga dua sudutnya sama besar. Segitiga sama kaki memiliki satu simetri lipat, namun tidak memiliki simetri putar.

3) Segitiga Sembarang

Segitiga sembarang adalah segitiga yang ketiga sisinya tidak sama panjang, sehingga besar tiap sudutnya berbeda-beda. Segitiga sembarang tidak memiliki simetri lipat maupun simetri putar.

Klasifikasi Segitiga Berdasarkan Besar Sudut

1) Segitiga Siku-Siku (Right Triangle)

Segitiga siku-siku adalah segitiga yang kedua sisinya membentuk sudut siku-siku (90°). Sisi yang tidak membentuk sudut siku-siku disebut sisi miring (hipotenusa).

2) Segitiga Lancip

Segitiga lancip adalah segitiga yang semua sudutnya lancip atau < 90°.

3) Segitiga Tumpul

Segitiga tumpul adalah segitiga yang salah satu sudutnya tumpul atau > 90°.

Persegi/Segi Empat

Persegi/Segiempat adalah bangun datar yang terdiri dari empat sisi sama panjang dan keempat sudutnya siku-siku (90°), sehingga total jumlah sudutnya adalah 360°. Segiempat juga disebut bujur sangkar.

Bangun datar Segiempat memiliki sifat-sifat loh, diantaranya :

a) Terbentuk dari empat sisi sama panjang

b) Keempat titik sudutnya adalah siku-siku

c) Memiliki dua diagonal sama panjang dan berpotongan yang membentuk sudut siku-siku

d) Memiliki empat simetri lipat

e) Memiliki empat simetri putar

Lingakaran

Lingkaran adalah bangun datar yang dibentuk dari kumpulan semua titik yang mempunyai jarak sama ke titik pusat lingkaran.

• Pusat lingkaran (P): Titik tetap pada pusat lingkaran
• Jari-jari (r): Jarak titik pusat ke tepi lingkaran
• Diameter (d): Garis yang ditarik dari dua titik di tepi lingkaran dan melewati titik pusat. Diameter lingkaran mempunyai panajng 2 x r.

Sifat-sifat Lingkaran, diantaranya:

a) Hanya memiliki satu sisi

Sisi yang dimaksud yaitu lingkaran yang berwarna hitam itu sendiri, tidak ada garis lain.

b) Tidak memiliki titik sudut seperti bangun datar lain

Titik sudut adalah titik yang terbentuk akibat pertemuan dua garis atau lebih. Sedangkan, pada lingkaran hanya terdapat satu garis yang membentuk tepi lingkaran itu sediri, sehingga lingkaran tidak memiliki titik sudut.

c) Memiliki simetri lipat tidak terbatas

Lingkaran dikatakan memiliki simetri lipat tak terbatas karena jika dilipat di bagian tengah lingkaran akan tetap membagi dua lingkaran sama besar, tidak terbatas hanya pada empat gambar di atas.

d) Memiliki simetri putar tidak terbatas

Jika dilihat dari gambar di atas, lingkaran selalu menempati posisi yang sama bila diputar bagaimanapun. Oleh karena itu, lingkaran dikatakan memiliki simetri lipat tidak terbatas.

CONTOH SOAL 

Contoh Soal dan Pembahasan Jumlah Sudut-Sudut Segitiga

Soal 1

Diketahui: ΔABC, ∠A = 2x°, ∠B = 3x° dan ∠C = 40°.

Tentukan:

a. nilai x

b. besar ∠A dan ∠B

c. jenis ΔABC

Jawab:

a. Untuk mencari nilai x dengan persamaan berikjut ini

∠A + ∠B + ∠C = 180°

2x° + 3x° + 40° = 180°

5x°  = 140°

x = 28

Jadi nilai x adalah 28

b. setelah mendapatkan nilai x maka besar ∠A dan ∠B dapat dicari

∠A = 2x°

∠A = 2. 28°

∠A = 56°

∠B = 3x°

∠B = 3. 28°

∠B = 84°

Jadi besar ∠A dan ∠B adalah 56° dan 84°

c. Jenis ΔABC adalah segitiga lancip yaitu segitiga yang ketiga sudutnya merupakan sudut lancip, karena sudut-sudut yang terdapat pada segitiga tersebut besarnya antara 0° dan kurang 90°

CONTOH SOAL SEGIEMPAT

1.. Sebuah kapal penangkap ikan berlayar lurus ke arah barat sejauh 40 km dari suatu pelabuhan, kemudian berhenti dan berhasil menangkap ikan sebanyak 2 ton. Kemudian kapal tersebut melanjutkan berlayar lurus ke arah selatan sejauh 20 km dan berhenti untuk menangkap ikan di sana. Setelah berhasil menangkap ikan sebanyak 3 ton, kapal tersebut berlayar lurus ke arah timur sejauh 40 km dan berhenti di sana untuk menangkap ikan.

Di daerah itu, kapal tersebut berhasil menangkap ikan sebanyak 4 ton. Setelah mendapat ikan yang cukup banyak, akhirnya kapal tersebut kembali berlayar lurus menuju tempat semula yaitu pelabuhan. Dari cerita tersebut, buatlah skema perjalanan kapal penangkap ikan. Bangun datar apakah yang terbentuk dari skema tersebut? Mengapa? Jelaskan alasannya!

Jawaban : 

Pembahasan :

Diketahui:

kapal penangkap ikan berlayar lurus ke arah barat sejauh 40 km dari suatu pelabuhan dan berhasil menangkap ikan sebanyak 2 ton Kemudian melanjutkan berlayar lurus ke arah selatan sejauh 20 km dan berhasil menangkap ikan sebanyak 3 ton Selanjutnya kapal berlayar lurus ke arah timur sejauh 40 km dan berhasil menangkap ikan sebanyak 4 ton kapal kembali berlayar lurus menuju pelabuhan.

Ditanyakan:

Skema perjalanan kapal penangkap ikan dan tentukan jarak antar wilayah tangkapan ikan yang letaknya sama dan sejajar?

Jawab : 

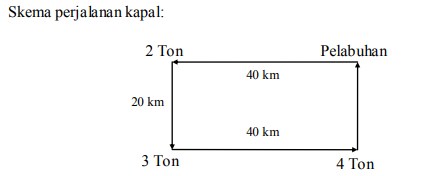
Bangun datar yang terbentuk adalah bangun persegi panjang. Karena pada gambar skema tersebut tedapat sisi-sisi yang berhadapannya sama panjang dan sejajar serta keempat sudutnya sama besar dan siku-siku.

2. Perhatikan gambar berikut!

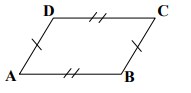
Segi empat ABCD adalah bangun datar jajargenjang. Diketahui ∠ 𝐷𝐴𝐵 = (𝑥 + 20)°, ∠ 𝐴𝐵𝐶 = (2𝑥 + 10)°, dan ∠ 𝐴𝐷𝐶 = 2𝑦°. Tentukan nilai 𝑥 dan 𝑦 serta besar ∠ 𝐵𝐶𝐷 !

Jawaban : 

Pembahasan :

Diketahui:
∠ 𝐷𝐴𝐵 = (𝑥 + 20)°
∠ 𝐴𝐵𝐶 = (2𝑥 + 10)°
∠ 𝐴𝐷𝐶 = 2𝑦°

Ditanyakan:

Nilai 𝑥 dan 𝑦 serta besar ∠ 𝐵𝐶𝐷 ?

Jawab:

∠ 𝐷𝐴𝐵 + ∠ 𝐴𝐵𝐶 = 180°
𝑥 + 20 ° + 2𝑥 + 10 ° = 180°
3𝑥° + 30° = 180°
3𝑥° = 150°
𝑥° = 50°
𝑥 = 50
∠ 𝐴𝐵𝐶 = ∠ 𝐴𝐷𝐶
2𝑥 + 10 ° = 2𝑦°
2. 50 + 10 ° = 2𝑦°
110° = 2𝑦°
55° = 𝑦°

55 = 𝑦
Maka nilai
𝑥 = 50 dan 𝑦 = 55
Besar ∠ 𝐵𝐶𝐷 = ∠ 𝐷𝐴𝐵
∠ 𝐵𝐶𝐷 = (𝑥 + 20)°
∠ 𝐵𝐶𝐷 = 50 + 20 °
∠ 𝐵𝐶𝐷 = 70°
Jadi besar ∠ 𝐵𝐶𝐷 = 70°

CONTOH SOAL LINGKARAN

Soal No.1

---

Sebuah lingkaran memiliki jari-jari sebesar 14 cm. Tentukan luas lingkaran tersebut ?
A. 154 cm²
B. 512 cm²
C. 654 cm²
D. 616 cm²

Pembahasan
L = π x r x r
L = 

227

 x 14 x 14
L = 616 cm²
Jawab : D

Soal No.2

---

Sebuah roda sepeda yang berbentuk lingkaran memiliki diameter sebesar 14 cm. Maka luas dan keliling roda tersebut adalah ?
A. Luas = 154 cm² dan Keliling = 44 cm
B. Luas = 512 cm² dan Keliling = 44 cm
C. Luas = 654 cm² dan Keliling = 64 cm
D. Luas = 616 cm² dan Keliling = 84 cm

Pembahasan
d = 14 cm
r = 

12

 x 14 = 7 cm

Untuk Luas Lingkaran
L = 

227

 x r x r
L = 

227

 x 7 x 7
L = 154 cm²

Untuk Keliling Lingkaran
K = π x d
K = 

227

 x d
K = 

227

 x 14
K = 44 cm

Jawab : A

Soal No.3

---

Pak Andi memiliki sebuah mobil yang panjang jari-jari ban mobil tersebut sebesar 21 cm. Saat mobil tersebut berjalan, ban mobil tersebut berputar sebanyak 200 kali. Berapakah jarak yang ditempuh mobil tersebut ?
A. 265 m
B. 412 m
C. 264 m
D. 178 m

Pembahasan

K = 2 x π x r
K = 2 x 

227

 x 21
K = 132 cm

Jarak yang ditempuh ketika ban mobil berputar 200 kali :
Jarak = Keliling × Banyak putaran
Jarak = 132 × 200
Jarak = 26400 cm
Jarak = 264 m

Jawab : C