persamaan logaritma dan sifatnya beserta contoh soal dan penyelesaian
- Dapatkan link
- X
- Aplikasi Lainnya
NAMA: ANGGUN INDAH SARI DARMAYANTI
KELAS: X MIPA 3
NOABSEN: 9
Rumus Logaritma
ac = b → ª log b = c
Keterangan:
a = basis
b = bilangan dilogaritma
c = hasil logaritma
Sifat Logaritma
| ª log a = 1 |
| ª log 1 = 0 |
| ª log aⁿ = n |
| ª log bⁿ = n • ª log b |
| ª log b • c = ª log b + ª log c |
| ª log b/c = ª log b – ª log c |
| ªˆⁿ log b m = m/n • ª log b |
| ª log b = 1 ÷ b log a |
| ª log b • b log c • c log d = ª log d |
| ª log b = c log b ÷ c log a |
Kegunaan Logaritma
Logaritma sering digunakan untuk memecahkan persamaan yang pangkatnya tidak diketahui. Turunannya mudah dicari dan karena itu logaritma sering digunakan sebagai solusi dari integral. Dalam persamaan bn = x, b dapat dicari dengan pengakaran, n dengan logaritma, dan x dengan fungsi eksponensial.
Persamaan Logaritma
Persamaan logaritma adalah persamaan yang peubahnya terdapat dalam bilangan pokok atau numerusnya.
Contoh : (i) log (3x – 1) = log (x – 15) , (ii) (x-1)log 16 = 2, dll Macam-macam bentuk persamaan logaritma :
- alog f(x) = alog p f(x)log a = g(x)log a
- alog f(x) = alog g(x) f(x)log g(x) = f(x)log h(x)
- alog f(x) = blog f(x) A.(a log x)2 + B(a log x) + C = 0
- f(x)log g(x) = p untuk A ¹ 0
Contoh soal :
Tentukan nilai x yang memenuhi pertidaksamaan 2log (2x-3) > 2log 5 !
Penyelesaian:
Kesimpulan : Nilai x yang menjadi penyelesaian pertidaksamaan harus memenuhi (1) dan (2) Jadi nilai x yang memenuhi adalah x > 4.
- Dapatkan link
- X
- Aplikasi Lainnya

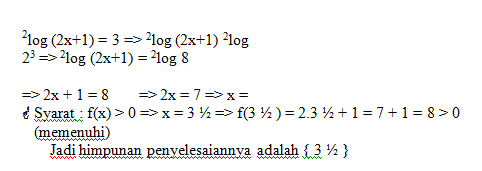
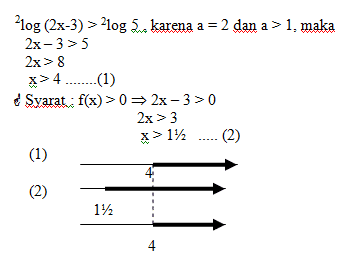

Komentar
Posting Komentar